2025.6.27

第19回試験問題について、ご意見・ご質問を頂戴しまして、ありがとうございます。

以下のとおり、ご質問へご回答申し上げます。

質問者からの文章は、一部を割愛させていただきました。ご了承ください。

---

■第19回・3級・問43

【設問】

白夜（びゃくや）と反対に太陽が地平線上に出てこない日を何と呼（よ）ぶか。

① 不夜（ふ や）

② 暗夜（あ ん や）

③ 闇夜（や み よ）

④ 極夜（きょくや）

【正答】

④ 極夜（きょくや）

【解説】
地球の極地域（きょくちいき）で、夜になっても太陽が地平線の下に沈（しず）まない、もしくは沈

んでも薄明（はくめい）が続く日を白夜（びゃくや）と呼（よ）ぶ。逆（ぎゃく）に、太陽が地平線

の上に出てこない日は極夜（きょくや）と呼ぶ。不夜（ふ や）は一晩（ひとばん）中明かりが灯（

とも）って街（まち）が賑（にぎ）わっている不夜城（ふ や じ ょ う）などで使われる。暗夜（あ ん

や）も単独（たんどく）ではなく暗夜行路（あ ん や こ う ろ）などで使われる。月のない暗い夜が闇夜

（や み よ）である。

【質問】

問題の選択肢として「④極夜（きょくや）」とされている一方で、今回の検定の出題範囲とされている

『天文宇宙検定公式テキスト３級2023～2024年版』（38ページ）では、極夜のふりがなが「ごくや」と

されています。大人を対象とした試験では特段の問題はないと思いますが、年齢層の低い方も参加され

る試験においては、ふりがなの違いは大きな影響が出るおそれがあるものと考えます。今回は正解が

「④極夜（きょくや）」になっていますが、選択肢として適切だったのでしょうか？

【回答】

『天文宇宙検定公式テキスト３級2023～2024年版』において、極夜（きょくや）とすべきところを極夜

（ごくや）と、ふりがなに誤植がありました。深くお詫び申し上げます。

本問は、全員正解として採点いたします。

3級試験は、中学生以上を受験対象と想定しておりますが、漢字のフリガナを正誤の判断基準とする年少

受験者が、一定数いらっしゃいますので、配慮の必要性があると判断いたしました。

---

■19回・2級・問50

【設問】

生物とウイルスのもつ共通の性質に関する説明文として正しいものはどれか。

【選択肢】

① 外界と境界によって隔たれた構成単位をもつ

② 核酸をもち自己複製を行うことができる

③ ミトコンドリアをもちエネルギーの産生を行うことができる

④ 自分自身で代謝を行うことができる

【正答】

②

【解説】

核酸とそれを包むタンパク質の殻からなるウイルスは、細胞のような構成単位はなく、ミトコンドリア

のような細胞小器官ももたず、自分自身で代謝をしない。一方で、核酸をもち、自己複製ができる生物

特有の性質をもっている。

【質問】

第50問の生物とウイルスの共通点に関する問題で、解答速報では　②核酸をもち自己複製を行うことが

できる　が正答となっていましたが、ウイルスは宿主に寄生することで増殖するので単独での増殖、自

己複製はできないのではないかと思います。

生物の細胞とは構造が異なりますが、ウイルスにも外界と隔てる膜のような構造は存在しているので

①外界と境界によって隔てられた構成単位をもつ　が正答に近いのではないかと思うのですが、いかが

でしょうか。

【回答】

ご指摘ありがとうございます。

この問題は２級テキストの記述通りの設問ですが、本件に関して、いままでではじめての鋭いご指摘で

した。ウイルスの定義は難しいのですが、現在の一般的な考えとしては、ウイルスは核酸とタンパク質

のみからなっており、細胞膜のような構成構造はないとされています。

「複製を行うことができる　が正答となっていましたが、ウイルスは宿主に寄生することで増殖するの

で 単独での増殖、自己複製はできないのではないかと思います。」ここも鋭いご指摘です。ご指摘のよう

に、ウイルスは“単独での増殖”はできません。しかしながら、寄生して核酸を宿主に入れることで、自分

自身の複製（自己複製）を行います。自己増殖・自己複製はしばしばひとかたまりで出てきますが、

ウイルスの場合はこれらが切り離されていて、設問やテキストでも、後者の自己複製のみが、取り上げ

られているものです。

以上の点から、この問題については、テキスト通りを正答とさせていただきますが、本公式テキストに

せよ、学校の教科書にせよ、テキストが常に正しいとは限りません。今後も疑問など生じたら、検定試

験時以外でも、いつでも質問をお寄せください。

---

■第19回・1級・問3

【設問】

3軌道長半径a、離心率eの惑星の運動を考える。図のように、惑星が近日点Aに来たときの公転角速度を

ω_{_1}、短軸上の点Bに来たときの公転角速度をω_{_2}とするとき、ω_{_2}/ω_{_1}はどのように表されるか。なお、

Sは太陽、Oは楕円の中心とする。

【選択肢】

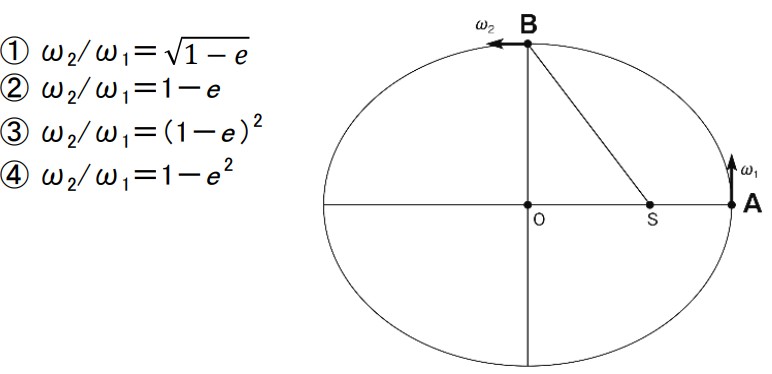
【正答】

③

【解説】

ケプラーの第2法則より、角運動量が保存する。惑星の質量をm、太陽からの距離をr、角速度をωとする

と、mr²ω＝一定となる。ここで、近日点Aでは、r＝a(1－e)、短軸上のB点ではr＝aとなる。したがっ

て、ケプラーの第2法則より、  ma²(1－e)²ω_{_1}＝ma²ω_{_2}の関係が成り立つ。これから  ω_{_2}/ω_{_1}＝(1－e)²

となり、③が正答となる。なお、楕円の2つの焦点をF（これは太陽Sの位置となる）、F´とすると、FB＝F

´Bである。長半径aの楕円は2つの焦点から距離の和が2aで一定となる点の軌跡で表されるので、FB＋F´B

＝2aとなるから、FB＝SB＝aとなる。

【質問】

次の点が気になりましたので質問します。

問題3の図の公転角速度ωのベクトル表示についてですが、角速度ではなく、接線速度ベクトル表示では

ないでしょうか。（うかつにも私は速度ベクトル表示と勘違いして1/2（ｒｖ）＝一定という「面速度一

定」の公式を適用して間違えてしまったのですが）本来角運動量保存則としてはL＝ｒ×ｐ（ベクトル表

示）＝r×ｍｖ（直交する場合）＝ｒｍｒω＝mr²ωと表示されますので、角速度は図面に垂直な方向に表

示されるべきではないでしょうか。

誤解を招きやすい図示であり、各速度ベクトル表示としては間違いではないかと思うのですがいかがで

しょうか。

【回答】
ご質問をいただき、ありがとうございます。

図の楕円に接するベクトルは、その場所での速度ベクトルです。つまり、惑星の運動方向を示している

にすぎません。速度ベクトルの付近に角速度ωを図の中に書き込んでいますが、ωはベクトル表記（太文

字）にはしておりませんし、問題文で「角速度ω」と明記しています。つまり、この図のωはスカラー

（大きさ）を表しています。図の速度ベクトルを角速度ベクトルと誤解されたということですが、そも

そも、速度と角速度の違いは、１級レベルでは正しく把握してほしい部分ですので、正答を含め、現行

のままで処理させていただきます。なお、角速度ベクトルは、おっしゃる通り、図に対して垂直上面を

向いておりますが、その場合はωも太文字のベクトル表記になります。

---

■第19回・1級・問32

【設問】

太陽以外の天体から飛来するX線を発見したのは誰か。

【選択肢】

① ブルーノ・ロッシ

② リカルド・ジャコーニ

③ マーテン・シュミット

④ アーノ・ペンジアス

【正答】

①

【解説】

太陽からのX線は1949年に検出されていたが、他の天体は遠いのでX線では観測できないと思われてい

た。ロッシは小さなガイガー計数管をロケットに載せて打ち上げ、1962年、はじめて太陽以外からの宇

宙X線を検出した。ジャコーニはX線天文学を発展させた立役者で、2002年のノーベル物理学賞を受賞し

た。シュミットはクェーサーの発見者、ペンジアスは3K宇宙背景輻射の発見者である。

【質問】

件名の通り、今回の1級32問についてお伺いしたい点がございます。

解答速報では、①のブルーノ・ロッシが正解となっており、解説でも1962年、初めて太陽以外からの宇

宙X線を検出した、とありますが、これに該当すると思われるブルーノ・ロッシの1962年の論文、

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.9.439

には②のリカルド・ジャコーニも名前が出ております。したがって②も正解なのではないでしょうか？

【回答】

ご指摘ありがとうございます。

宇宙X線観測の研究全体の主導者はロッシで、天文学史的に、宇宙X線の発見者はロッシとされていま

す。設問もその意図でしたが、明瞭ではありませんでした。

またご指摘のように、1962年の最初の論文には、ジャコーニも入っており、選択肢には紛れがありま

した。以上の点から、本問題については、全員正解とさせていただきます。